Visions tétras

Même s’ils se défilent, les propriétaires rayonnent

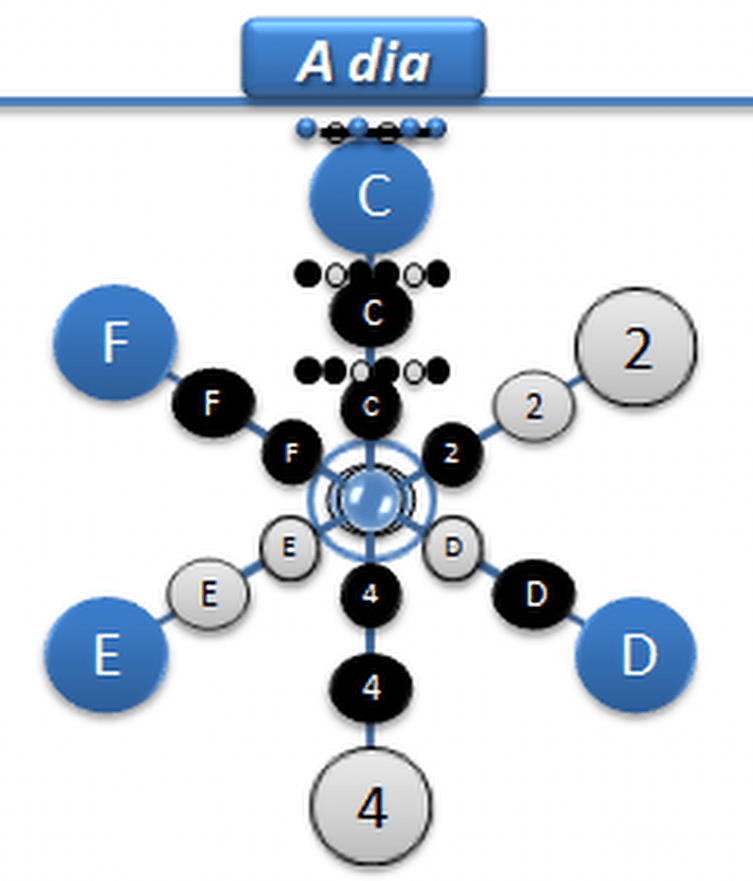
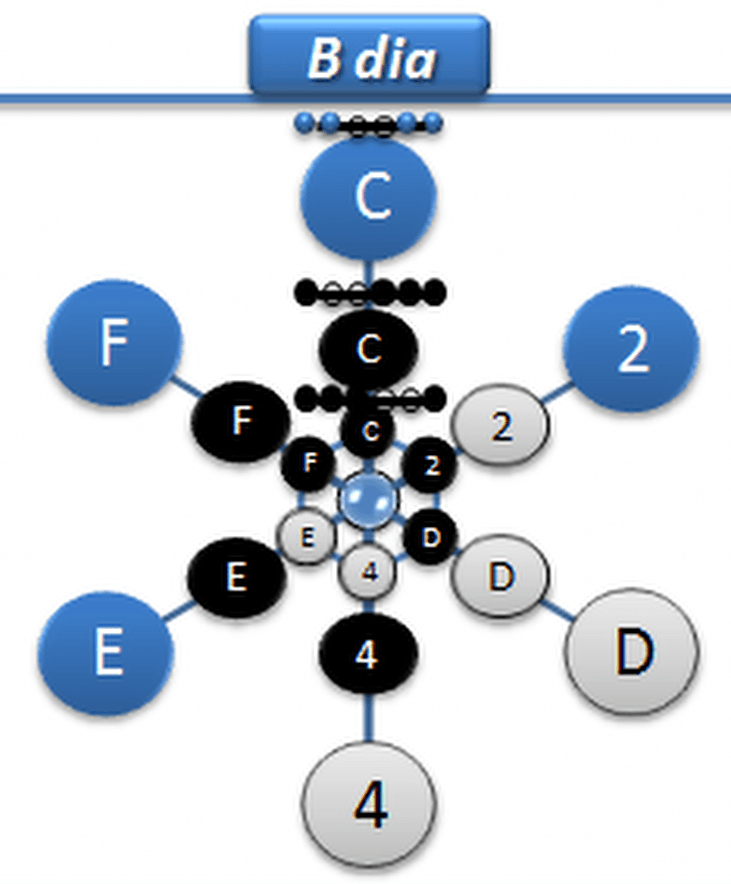
Le bar du delta garde le grade original. Il donne le niveau à chaque classe tétra.

Chaque rayon à une valeur, ainsi que chacune des classes

Ce qu’est l’étoile :

Par division, on peut mesurer une étoile à l’aide d’un polygone. Qui va établir un nombre réel de côtés liés à une seule énergie relative à l’objet tétra par exemple.

D’autant plus, par la disposition de l’objet tétra, qui contient des intervalles. Dont l’harmonie positive va caractériser une occurrence irrégulière et objective.

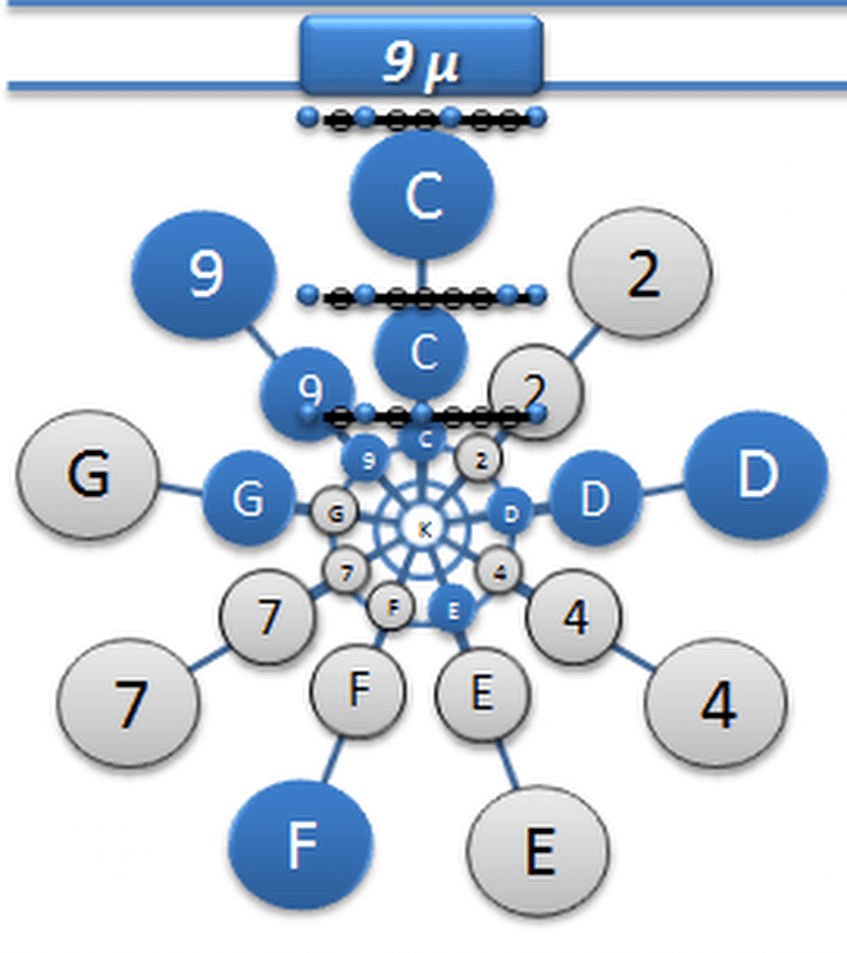
La relativité des formes de base. La gamme naturelle donne une série de deux polygones. Un heptagone pour les notes relatives absolues. Un pentagone pour les intervalles réguliers vides. Tous deux se complètent, et dessinent les vecteurs liés à un rayonnement de douze côtés. (360°/12 = 30°)

Utilisation des points d’angle, se fait en raison des objets tétras. Ici, le tétra s’est adapté, car on ne tient compte que de ses notes. Qu’on a mis à leurs emplacements, dans les différentes sphères. Dans cet exemple à gauche, les tétragones complètent les divisions dodécatoniques. Bien qu’il subsiste un décalage avec les tétras utilisés, ici. Un raisonnement de probabilité intervient en faveur de cette évolution. Sur le fait d’une exponentielle évolution, dans un milieu conditionné. 

Dans cet exemple.

Les points cardinaux ont été précisément suivis, faisant aussi abstraction des réalités absolues des notes des tétras. De plus, cette figure est diatonique à l’objet. Puisqu’il présente un développement modal naturel, un même objet à plusieurs niveaux. Les combinaisons sont riches en complexités, et dans l’ensemble la découverte est à la hauteur de la connaissance. Ou, c’est la connaissance qui développe les sujets à découvrir.

Quelques modèles d’assemblage, ils sont diatoniques ou typiques. Voire atypiques.