Les gammes fondamentales

Elles ont été classées dans un ordre simple, particulièrement nommées en raison de chaque formule gammale.

Le tableau ci sous, se constitue d'un nom de gamme et de sa formule chiffrée.

Le nom servira pour l'adressage, la formule envahira la variable Maj Num (num).

Exemple : Maj Num () de b3 ⇿ (1, 0, 1, 1, 1, 1, 0)

Exemple : Maj Num () de b4 ⇿ (1, 0, 0, 2, 1, 1, 0)

Nous avons bien (ci-sur), une série de formules numériques

Se présentent à vous en tant que famille numérique, en rapport du dé a deux dimensions ; Soit, quatre spécimens bien frais et dispos. Le profil humanise cette progéniture et ainsi dévoile le mystère de camouflage, du premier membre. Le premier sinistre est quand on les voit de face, invraisemblable !...

Ils se transforment en formules numériques… coquillées & crustacés...

Comme quoi on peut tout dire. Et si vous voulez voir la photo de famille, cliquez Mr & Ms POOLs

Voici, la famille des POOL au complet \

66 énergumènes piailleurs en façade.

Je reviendrai, quand je serai plus apte à détailler

ce fabuleux phénomène (voir photo) 

Logmodoctave

Logarithme en Modulation d'Octave

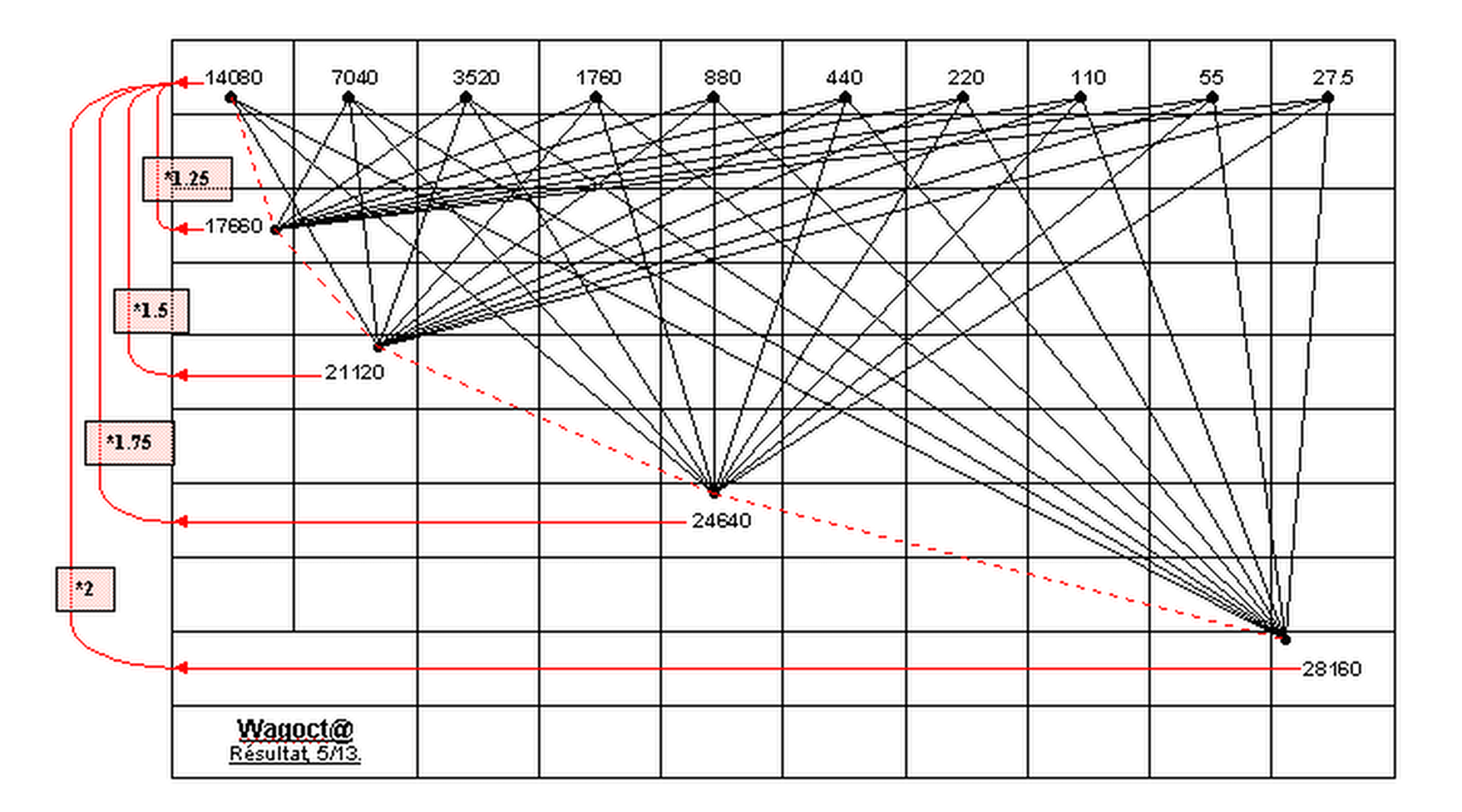
Sur la ligne supérieure sont les primitives. Elles produisent quatre lignes équidistantes.

Comment commencer : « Nous avons le LA (A) 14080 htz.

Ensuite, nous avons le produit (C) 17660 htz. Qui est le résultat de ; A*1.25.

En prenant, par exemple, le produit (#F) 24640 htz. Sera de, A*1.75.

Calculer les primitives : Nous savons que l'octave inférieure de A 14080 est A/2. 

C'est ainsi que s'est initialisée la ligne supérieure, comme base principale.

De là, ces valeurs peuvent calculer les équidistances.

Il y a 10 octaves, donc dix primitives. Et de (#D) 21120, partent dix traits ;

Qui ont le même algorithme que l'octave, *fois deux le multiplicateur.

Si, (14080*1.25) = (7040*(2*1.25)) = (3520*(2*(2*1.25))) = (1760*(2*(2*(2*1.25)))) = = = 17660.

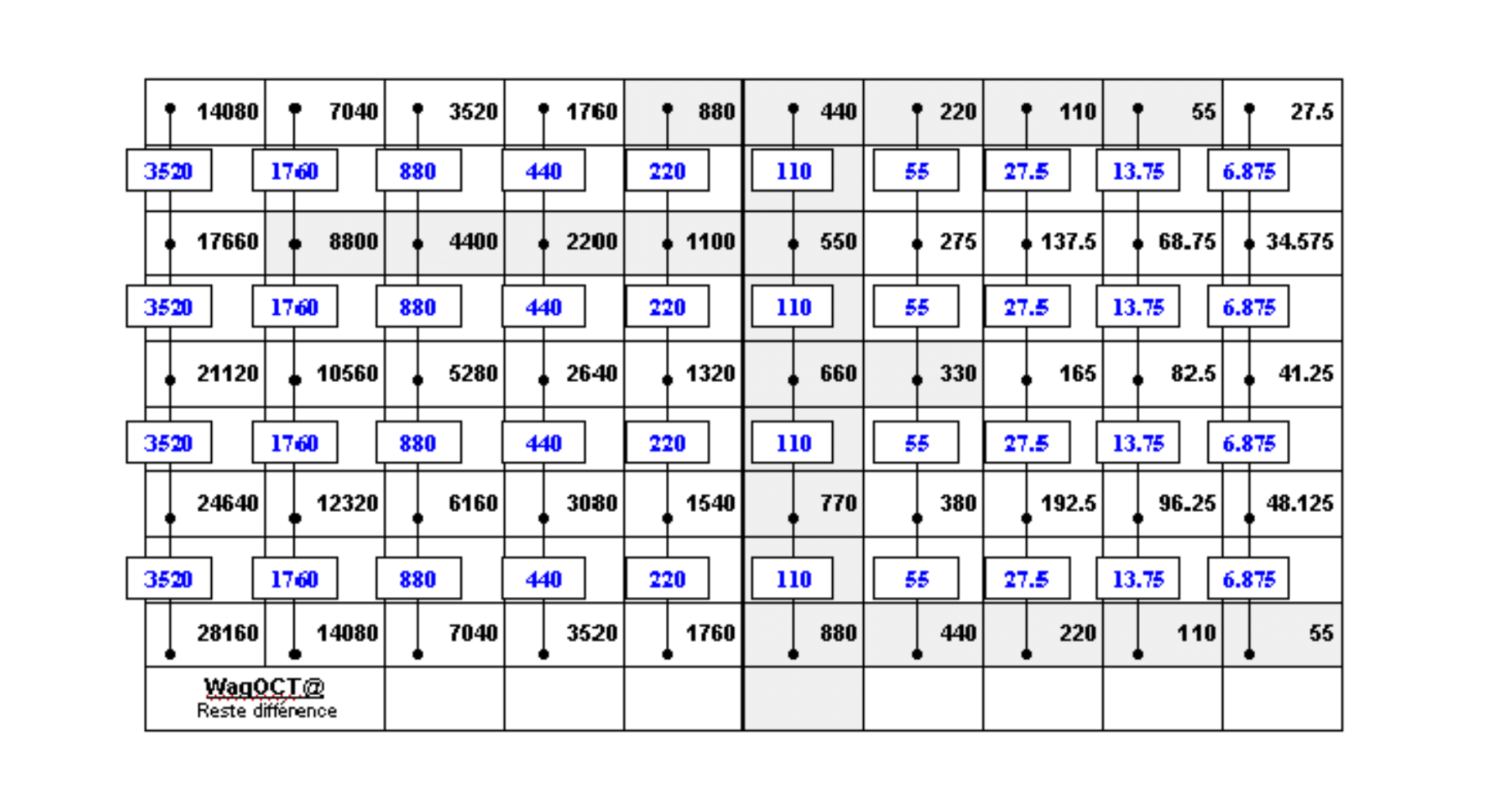
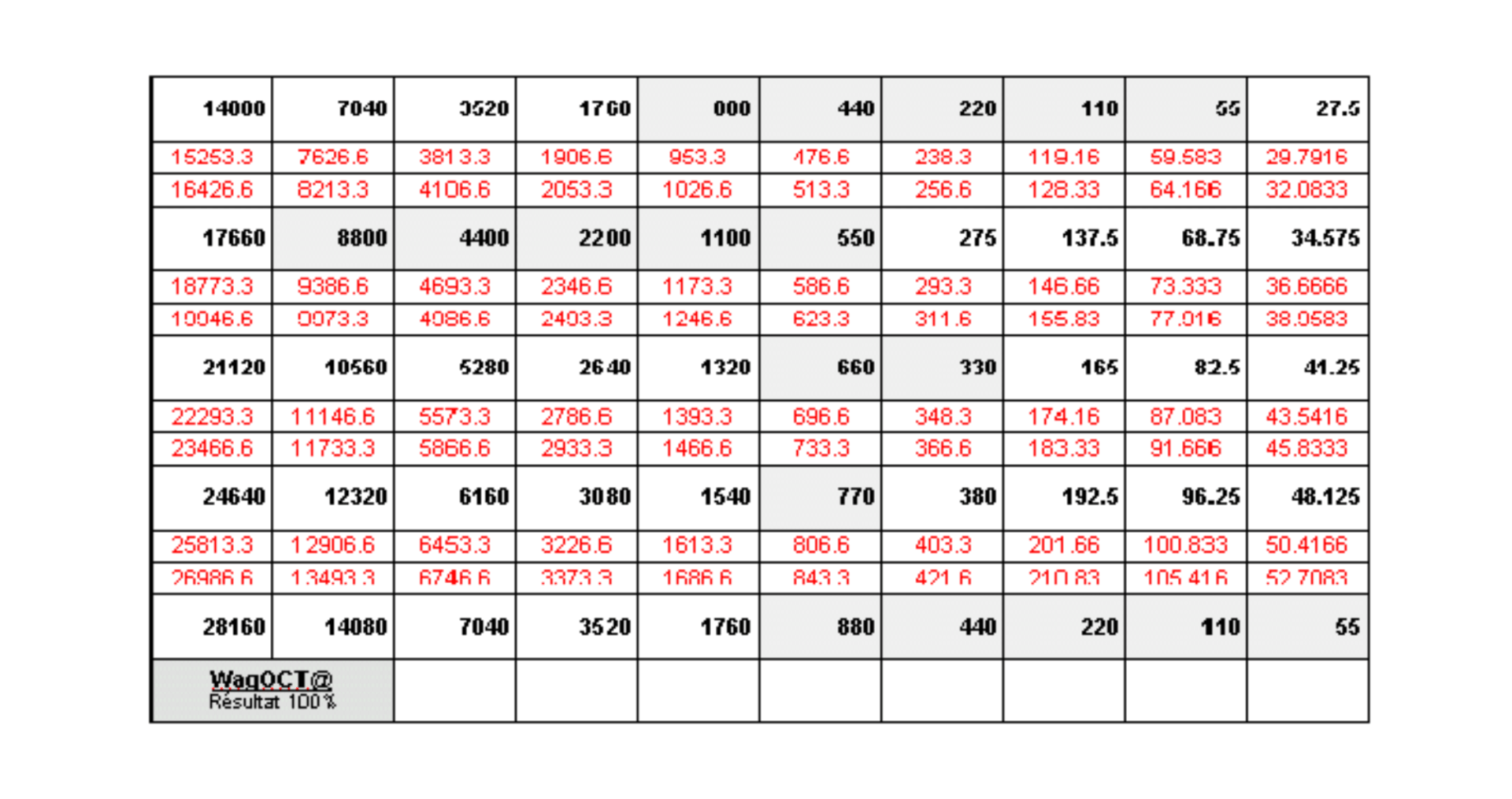
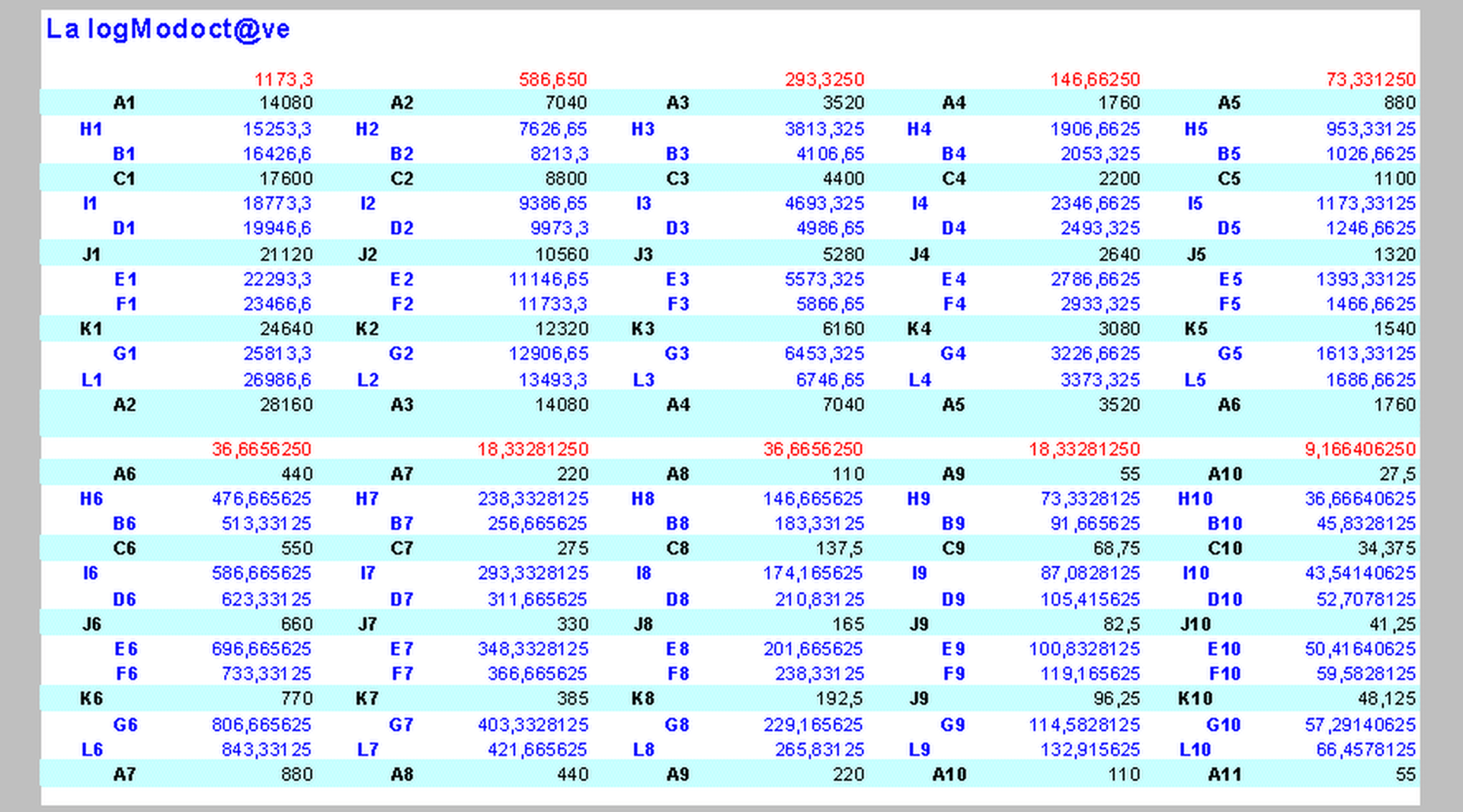
Voici Wagoct@; 

On retrouve les fréquences de ci-dessus, les lignes des entiers sont complètes.

Encadrées et bleues, les fréquences htz, données par différence.

À savoir, le traitement du graphique mathématique de ci-dessus, est applicable à chaque octave.

Nous sommes sûrs d'avoir cinq notes justes.

Premier Exemplaire Approche Octave Sûrement Imprécis                                                  Et pour plus de précision(s)

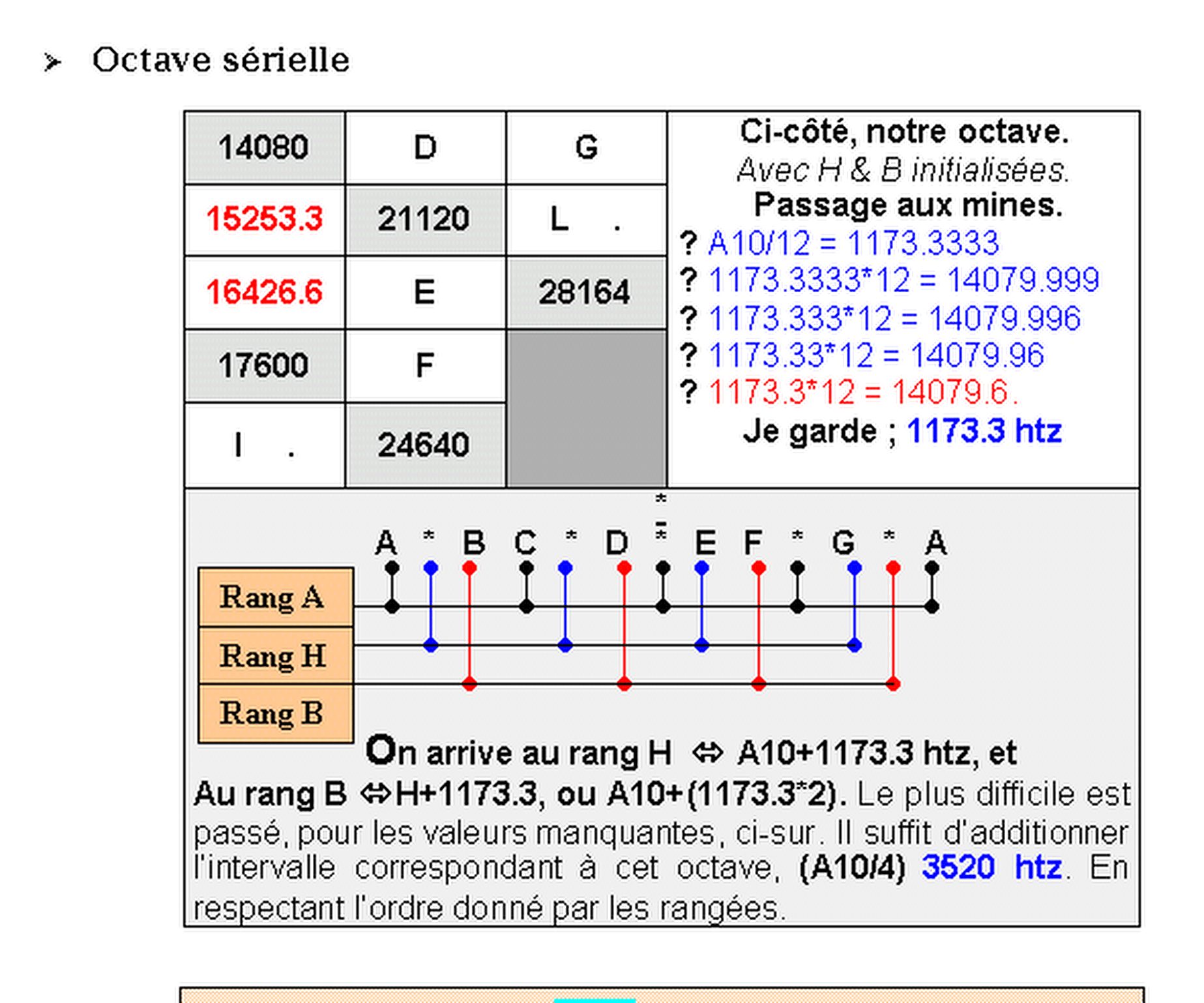
Découvrez la relation valable, entre le mode octave (double) & le mode calculé, sur l'image du bas de page. 

Une information m'est arrivée, et j'ose la donner. C'est cela même qui a provoqué ce test-ci-gauche.

BACH en est le créateur, passage au mode tempéré. C'est parler des intervalles exprimés en nombre de HERTZ (M.).

Il s'agit de diviser l'octave en 12 parties égales, d'où le tempérament.

 LES DIFFÉRENTS TESTS : 

2^(1/12) D'abord sa valeur initiale Ensuite la liste dans l'octave. Ça tombe juste, voyez les décimales 

2^(1/175) Valeur initiale commatique 

175^12 Nombre de gammes commatiques 

440/12 Valeur initiale non tempérée 

(440/12)*12 Ça tombe juste aussi

Les détails qui frappent ...